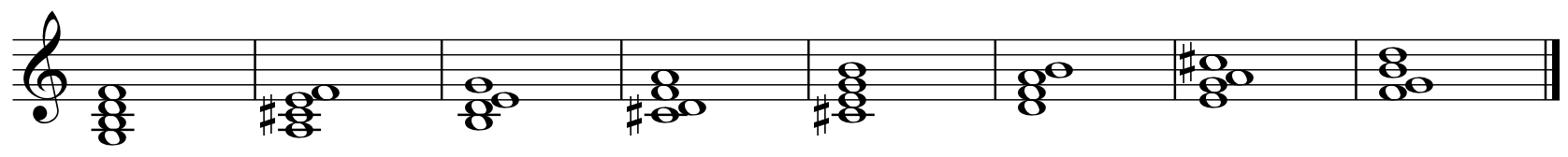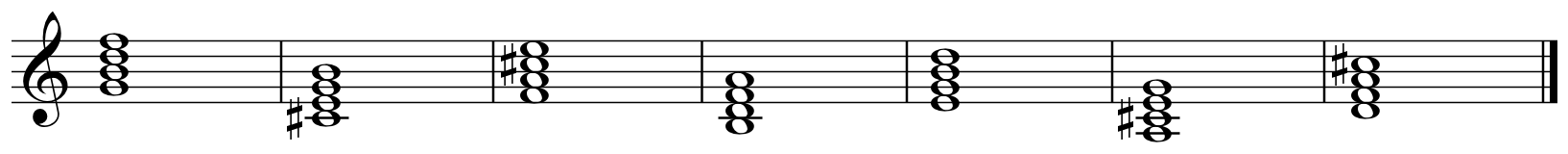This study is aimed at the jazz musician who is interested in expanding their harmonic horizons, especially the pianist, guitarist or vibist who wants some new ideas for block chords, but also for anybody who wants a new vocabulary for approaching playing lines. All the chord formations discussed here can be arpeggiated in various ways as a practice tool, and the modal approach to the scale forms an interesting basis for choosing notes in a solo. Maybe I should point out that I am not advocating an arpeggio-based "play as many notes as you can" type of approach to soloing. Just because you absorb all the ideas in this study doesn't mean that you should play them all the time. But I advocate knowledge in general, and a musician (like anybody else) makes progress by challenging what they know.

Please don't be confused by the algebra I use sometimes. Normal chord notation specifies a root note - of course! But very often, improvisers want to free themselves from key constraints, and in order to use an idea in all keys, they need a way of visualising the idea without reference to a root. This is why I use terms like X7(b9). Similarly, if I am talking about harmonic movement, then I use semitones, rather than conventional intervallic names, to describe this. So instead of saying...

... I use X7 => (+5) instead, which seems easier. If I want to describe a pair of chords without reference to key, I can use the same method:

which describes for example the sequence Bb9 => Cmaj7, or D9 => Emaj7, etc.

To make the semitone movement easier to visualise, I rarely use a higher number than 6, which describes movement of a tritone. In other words, if I describe a movement as (-3), it simply means from, for example, C to A, without necessarily being "down" in pitch.

This may also be of interest to composers interested in using the melodic minor in unusual ways. The section on movement within a mode could easily be employed in a modern chorale, or in writing for a string quartet.

If you want to discuss this project with me, get in touch here.

• How the substitution process works
• The four scalar substitutions for the dominant seventh
• Descriptive notation
• Intra-modal chord movement
• Conceiving substitutions over a chromatic resolution
• Resolving to a minor key
• Reharmonising standards

How the substitution process works

The melodic minor scale is often used as a modal substitution for a dominant seventh chord.

Of the seven modes of the melodic minor, four are suitable for this purpose. The first and third are discounted because the seventh is raised; and the sixth has no major third and no natural fifth. This leaves II, IV, V, and VII.

The four scalar substitutions for the dominant seventh

Given that these modes are useful harmonically in the dominant context, it follows that there are theoretically four groups of seven chord substitutions. In the following example, G is given as the root.

The following table shows this same information in terms of the relationship between the dominant chord and the melodic minor scale used.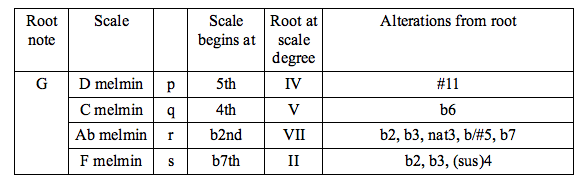

The following table gives the four scalar options in all keys.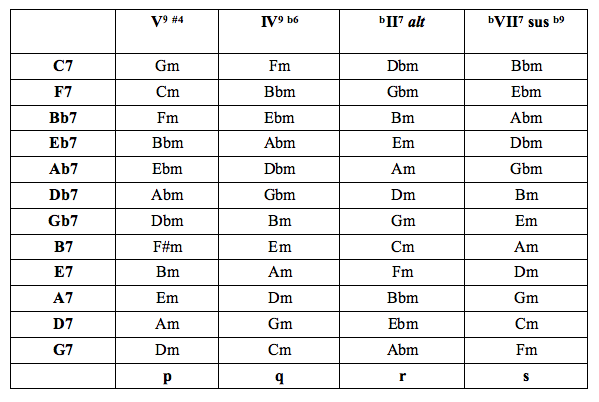

Descriptive notation

Since we are dealing with a limited number of options for scalar substitution, I have given them the abbreviated names p, q, r and s. This helps us to develop a simple descriptive notation for upper structure chords in this system, and thereby to easily transpose them.

Rather than Abmaj7^#5 / Bb = Bb9 ^{(#11 13)} we give Bb7 p(iii)

Where p refers to the choice of V melmin, and iii refers to the degree of the melodic minor scale used as an upper structure.

Similarly:

We give C7 s (i), (iii), (i), (vi)

Thus the whole spectrum can be represented in the following manner, where X7 is any dominant chord:

Intra-modal chord movement

Once you know what scale to use, the next step is to have an understanding of the systems by which virtual movement can be applied to the given modal environment, especially if the mode is to be used over a longer period. These consist of:

• Parallel (horizontal) movement
• Vertical movement
• Pseudo-functionality and -plagality

All of these processes work well in both directions: pseudo-functionality implies plagality, just as both horizontal and vertical chord movement can, strangely, both ascend and descend.

Parallel chord movement:

Vertical movement on a lattice built in thirds:

Pseudo-functionality is the same phenomenon one finds in diatonic sequences, where the cycle of fifths is approximated as nearly as possible without leaving the modal environment.

When reversed, this gives what I call pseudo-plagality.

If you are like me, and want to really twist your brain, try visualising the following while substituting a dominant chord. Even better if you can stand on your head at the same time.

• Ascending parallels descending
  
• Descending parallels ascending
  
• Ascending vertical sequences with minimal voice-movement
  
• Descending vertical sequences with minimal voice-movement
  
• Pseudo-functional sequences in parallel
  
• Pseudo-plagal sequences in parallel
  

Conceiving substitutions over a chromatic resolution

The musician using melodic minor substitutions over the cycle of fifths needs a system to visualise voiceleading possibilities. Let us suppose that a single substitution is to be used. That is, for example, G7 p/q/r/s (i) to C7 p/q/r/s (i).

The following chart illustrates internal transposition in the secondary chord structure (the melodic minor forms.) I have put parallel movement in italics, because in functional harmonic movement you don't really want parallels.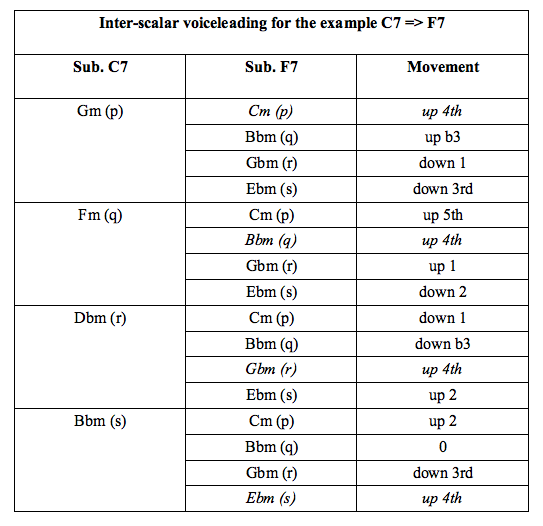

Alternatively, one can start with the desired intervallic relationship between the internal voices and list the possibilities for a perfect cadence. The forms in the square brackets refer first to that of the resolving dominant, and then to that of the landing-dominant.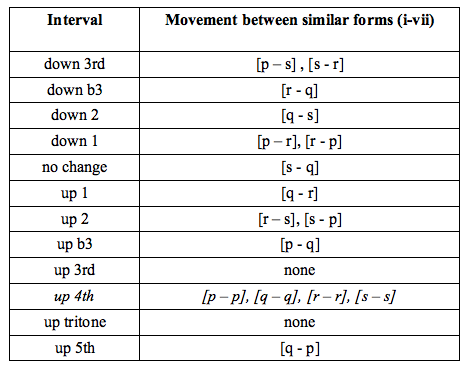

What does this tell us? That, in our melodic-minor-centric world there are 16 harmonic solutions to the substitution of two dominant chords in functional sequence. However each of these harmonic solutions can be expressed in a nearly infinite number of ways. No excuses, then, for always playing a resolution in the same way!

Resolving to a minor key

It is also useful to be aware of substitutions for a resolution to a home minor key. Only two melodic minor substitutions are used for a dominant chord with a flat ninth. In the following tables, substitutions for C7b9 resolve to Fm. Degrees i, iii, and vi retain the tonality of the minor they are derived from, and are therefore listed as landing chords. The general parallel process may be described as follows: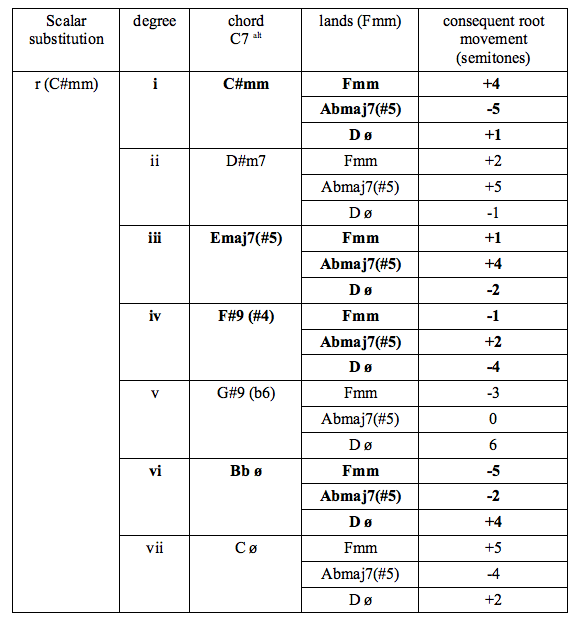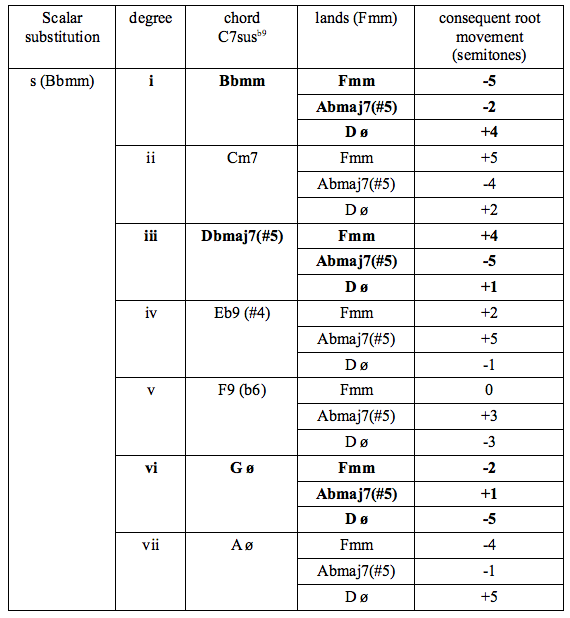

I included all the possible variations for the sake of completeness, but the ones given in bold are the primary voicings which maintain the original harmonic sense more strongly, by including the (raised) third and the seventh of the dominant chord in the upper-structure.

Here, then, is a list of substitutions for ( C7^b9 => Fm ) , where these preferred upper-structure possibilities from Vr and Vs are combined in ascending order. Parallels are in bold. These are now arguably desirable as the primary progression is not parallel.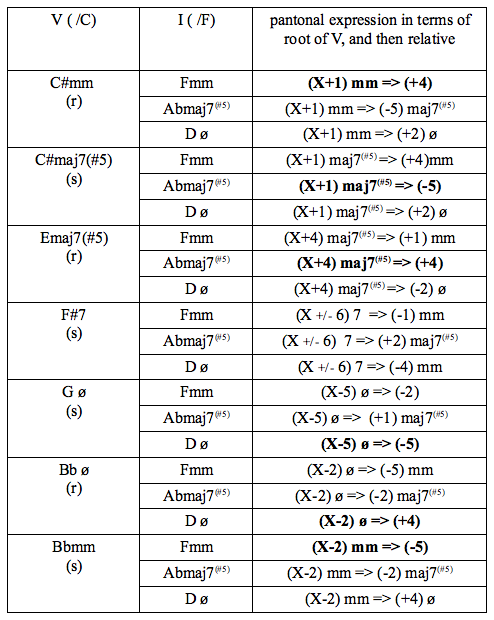

Reharmonising standards

Examples coming soon. Mind you, if you got this far, you can probably do it yourself, can't you? :-)

Soon I will also be adding various sound clips, so check back! Thanks for reading!