Did you ever wonder what happens if you take the concept of playing in unusual time signatures to its logical extreme? This is what this project is dealing with. Most jazz musicians have some experience with at least five-four time, or seven-eight time. Many classical composers use time signatures extensively, a few very strictly, like Bartok in later books of Mikrokosmos, where this is often influenced by Bulgarian and Hungarian folk music. But very few use this as a starting-point for constructing a rhythmical world where the time signature is simply a starting-point for building layers of concurrent cross-rhythms, especially in improvisation.

I became hooked on making an asymmetrical pulse achieve the same flexibility as regular four-four time. This leads to problems for an improviser: how to avoid a mechanical approach to phrasing in a complex context? Or how can one make use of the mechanical in creative improvisation? Starting with short pulse formations, such as 7 or 11 quavers, I began to learn how to build cross-rhythms in various ways: by combining quavers regularly, which gives rise to a polyrhythm; by combining beats, which gives a "fluid" polyrhythm, where the internal structure of the cross-rhythm is in continual flux; and finally by combining the beats within the polyrhythms themselves.

What does the musician gain from this? Among other things, the following:

• Heightened awareness of rhythmic structure
• The ability to improvise confidently and fluidly in any time signature
• Strengthening pattern visualisation and memorisation
• Experience of constructing and learning polyrhythms analytically

I have some experience of passing on these techniques through workshops to musicians, and also to dancers of various kinds, that is to say, modern dancers (working with "movement periods"), tap dancers, and more. I am also happy to say that several excellent musicians have also worked with these ideas in their own way, in compositions and improvisations, such as Rune Mandelid and Ulrik Thorsrud.

This is the abridged version of ideas I have been working on for many years. If you have questions or other input then please get in touch through the website.

• What is complex pulse?
• Limitations of time signatures
• Notation and "Q def"
• Beats and comma beats
• Combining beats and the use of "G"
• Matrices
• Three types of Rhythmic Circles
• Learning advanced polyrhythms

What is complex pulse?

Pulse in music is what you tap your foot to, that is, the underlying metric basis of the music. In most music the pulse is either simple or compound. Examples of simple pulse are 4/4 time, or 3/4 time. In each case the unit which is felt as the pulse is the crotchet. This would be the case however many crotchets there were in the bar.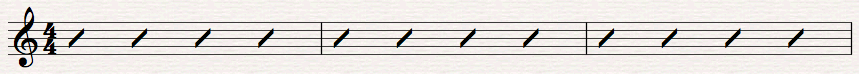

When each beat is comprised of a unit other than the crotchet, the music has Compound pulse. An examples of this is 6/8 time. This means that there are two dotted crotchets to the bar.

Complex pulse is where these two units are mixed in a longer pattern, which itself repeats. All complex pulse time signatures can be represented by groups of twos and threes. This means that there is not usually an easy way for the audience to tap their feet, though I have known audiences who tried!

Beats consisting of crotchets, or 2 quavers, are called "short" beats. Beats consisting of three quavers are called "long" beats. The simplest complex pulse formation is alternating short and long beats, or 5/8 time.

Limitations of time signatures

Time signatures are fine for "normal" music, but as soon as the pulse is irregular, musicians get just as worried as doctors. They need to know the way the bar is broken down. If the time signature is 11/8, that is not enough information. How is it 11/8? Using short and long beats you have nine possibilities, each of which has a different groove:

Obviously, the more quavers per bar, the more permutations there will be, so it is necessary to find a convenient way of absorbing the pattern at a glance. I usually dispense with the lower number in the time signature and replace it with Q. These days, the question of how many times a pulse unit fits into a semibreve no longer seems strictly relevant.

Notation and "Q def"

You can use numbers for referring to patterns, but when writing music I use triangles for long beats, and slashes for short. These are particularly useful when written over the bassline, for example, helping to clarify how it fits the pattern. I call this a pulse map, since it helps you find your way around.

This piece is written simultaneously in common time and in the above rhythmic pattern, where I improvise in 13/8 and the other guys play in 4.

I use "Q def" as short for "definition of the shape of the bar in terms of quaver groupings". Anything for the easy life. So the above bar-type can be described succintly as follows:

In my compositions I usually define the groove at the beginning of the piece. If the piece contains several different patterns then I define them all, also at the start. This gives musicians the chance to prepare the groove before they need to start learning the specifics of a line (or it can be used by itself as a structural device in a composition, more later).

In practical terms the challenge is obviously to be able to become good enough at feeling long and short beats in relation to each other that one does not become confused by the lack of a straight pulse. This sounds easy but actually takes a fair bit of effort. One useful way of practising is to a straight metronome beat, allowing the beats to fall on and off the click, but it is worth spending some time just with the quavers, and playing slowly. The point, especially with shorter patterns, is to avoid phrasing the second bar differently from the first just because it is "off" the metronome beat.

In the example above, I first show the metronome as a cross-rhythm (I encourage this approach) and then the complex pulse as a rhythmic pattern in a simple pulse framework. Clearly two bars of the complex pulse xQ can always be shown in simple pulse as xC, but bars do not always go in twos, and the metronome in the complex context does not necessarily have any musical function.

Beats and comma beats

Okay, the time signature is 11Q, but how many beats are there in the bar? Not eleven! "Beats" in this sense are related to the pulse, and the pulse is made of twos and threes. As shown above, there are nine ways of building an 11Q bar with twos and threes. Five of these have 5 beats in total (1 long and 4 short) while the other four have 4 beats (3 long and 1 short). I refer to this as B. So, under normal circumstances, if Q def [ 3 : 3 : 2 : 3 : 2 ] , then B=5.

This is where comma beats come in. The point is that a long beat, worth 3 quavers, can be played as 2 and 1. It is still a single long beat in structural terms, but becomes worth two beats when assigned to a line. Clearly this makes using "B" much more flexible, since every long beat in a pattern can either be worth one or two beats. You could say that B varies by the number of long beats in a pattern. In the example above, which includes three long beats, B varies from 5 to 8. More on this subject under the section on matrices.

As a matter of fact, the arrangement of beats in the bar is the defining factor in the creation of a groove. For example, the following pulse formation is one I have used quite extensively:

Here is a piece I wrote in this pattern:

Combining beats and the use of "G"

Combining beats in regular patterns over a complex pulse formation gives some interesting results. This can be used as perhaps the easiest way to play crossrhythms "on the beat", that is, only requiring the internalisation of one pattern to apparently achieve two, but is also a useful compositional device for generating phrases that cross the pulse while leaving the original groove intact.

If beats are combined in pairs, G=2. If in threes, then G=3. This is a useful shorthand way of describing a crossrhythm.

Below I give various permutations for the pulse shape described by

This process can be used to generate patterns to strengthen understanding of, or explore complex crossrhythms within, a particular pulse formation. But it is also potentially a structural construct, where the internal cohesion of rhythmic entities can also be expressed by melodic repetition.

The example above is the bassline from my piece "Buchan's Steps". (If you have read John's book you will understand the title!) This is a good example of the use of G. The pattern is the same type of 13Q as before:

Another example is the bassline from "Procrastination", another tune I wrote for Sphinx for our album Harmonogram. The bassline at the beginning is the same metrical structure, but only the first phrase of each melodic grouping.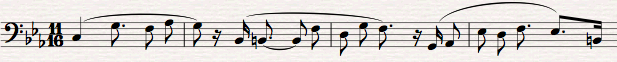

Matrices

You can use B for giving new twists to old material. You can map the material onto the matrix. This is easiest when the number of beats is the same in the matrix, but anything goes. You can also tie some of the beats in the matrix together and have beats of two, three, four or five or more quavers.

Here, I mapped the old Paul Desmond classic onto two different matrices, each having five beats.

You can also alter the matrix in the course of the composition, or find a generative process from one matrix to the next (then you are thinking like me!)

Three types of Rhythmic Circles

"Rhythmic Circles" is a general term I give to cross-rhythm in complex time. There are three main types:

Quaver-based rhythmic circles (QRO)

This is the superimposition of regular numbers of quavers onto the micropulse, where the implied secondary pulse (macropulse) is defined by the period of the CR. For example, playing 5Q CR over 7/Q time. So although the 1P is complex, the 2P is only compound. (Groupings according to Q). Here the CR may well have no relation to the micropulse, and may even be equal to it (see the section on polyrhythms).

Beat-based rhythmic circles (BRO)

This is the most frequent type employed in this study; the regular combination of beats within the primary pulse pattern to form a cross-rhythm, directly related to, and derived from, the primary pulse. Here both the primary and the secondary patterns are complex. Essentially the creation of BRO takes place when using values of G.

Tempo-based rhythmic circles (TRO)

Where two or more concurrent tempi are set for a piece, these being related in the form of a ratio, one of these may be selected as the primary pulse. The value of a crotchet in the two patterns is not the same; for example, a bar of 4/C at the primary tempo may occupy the same period of time as a bar of 5/C in the secondary, the tempo difference therefore being expressed as 4:5. Should the beats in 2P be rearranged, we have a TRO.

QROs are structurally polyrhythms. BROs are looked at in the section about the use of G. Here is a fairly simple example to illustrate how to use TROs (these are not necessarily used in the context of complex pulse). This TRO comes from the polyrhythm 4:3. If you can't hear the subdivisions it sounds pretty wierd. Actually it ends up being 16:15.

Learning advanced polyrhythms

In this context, by polyrhythm I mean two or more constant, measurable tempos, tempo A and tempo B, which coincide after a cycle AB. The simplest polyrhythms are standard fare in music education, but it is possible to expand one's awareness of polyrhythm by simply looking at the mathematics.

To find 4:3, for example: in 4C time one groups quaver triplets in fours; and in 3C time one groups semiquavers in threes.

Exactly the same process applies to all polyrhythms. The only complicating factor is length: it is easy to memorise 4:3 as a pattern because it is so short. What about 7:5? Once again, the key is awareness of complex pulse, and the ability to think in any number of quavers. If you can think in both 7Q and 5Q (the specific Q def doesn't matter here) then you can play this without too much trouble.

I don't think that there is any other equally effective way of practising complex pulse as analysing and working on polyrhythm. Additionally, I think there are few better meditation aids than working on feeling (and not just counting) polyrhythms.

Any comments? Feel free to send me a mail, contact details on the website.

© David Arthur Skinner